
في عالم البرمجة وعلوم الحاسوب، نواجه العديد من المشكلات المعقدة التي تتطلب حلولاً فعالة وسريعة. هنا يأتي دور الخوارزميات الاستكشافية(Heuristic Algorithms)، وهي أساليب ذكية تساعدنا في إيجاد حلول جيدة ومقبولة للمشاكل، حتى وإن لم تكن مثالية دائماً نظرا لعدم وجود حل مثالي للمشكلة، أو أن إيجاد هذا الحل يتطلب جدا ووقتا كبيرين للوصول إليه. دعونا نستكشف هذا العالم المثير ونفهم كيف تعمل هذه الخوارزميات وأين يمكننا استخدامها.
ما هي الخوارزميات الاستكشافية:
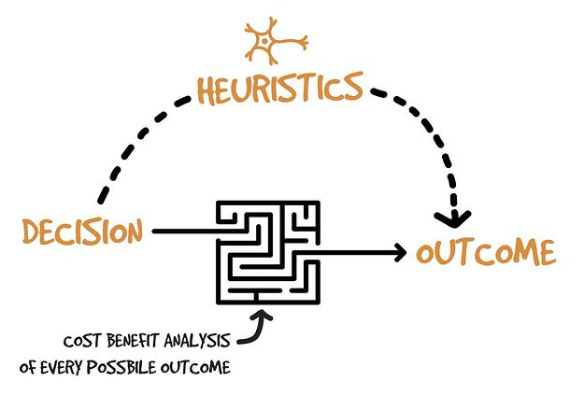
الخوارزميات الاستكشافية هي طرق حل للمشكلات تعتمد على الحدس والخبرة بدلاً من الحسابات الدقيقة. يمكننا تشبيهها بالطريقة التي نتخذ بها قرارات سريعة في حياتنا اليومية للحصول على حلول “جيدة بما فيه الكفاية” ضمن فترة زمنية معقولة. على عكس الخوارزميات التقليدية التي تسعى للحصول على حل مثالي. تركز الخوارزميات الاستكشافية على إيجاد حل قريب من المثالي عندما تكون سرعة الحل أكثر أهمية من دقته.
على سبيل المثال، عندما نختار طريقاً للذهاب إلى العمل، غالباً ما نعتمد على خبرتنا السابقة بدلاً من حساب كل الطرق الممكنة بدقة.
لماذا الخوارزميات الاستكشافية:
- التعامل مع التعقيد: بعض المشكلات البرمجية معقدة جداً بحيث يصعب حلها بشكل مثالي في وقت معقول.
- توفير الوقت والموارد: في كثير من الحالات، نحتاج إلى حل سريع وجيد بما فيه الكفاية، وليس بالضرورة الحل الأمثل المطلق.
- مواجهة عدم اليقين: في بعض المواقف، قد لا تتوفر لدينا جميع المعلومات اللازمة لاتخاذ قرار مثالي.
كيف تعمل الخوارزميات الاستكشافية:
تتصف هذه الخوارزميات عادة بعدد من الخصائص التي تجعلها مناسبة لحل الكثير من المشاكل، مثل:
- السرعة Speed): توفر حلولًا سريعة للمشاكل المعقدة.
- التقريب(Approximation): بدلاً من البحث عن الحل الأمثل، تسعى للحصول على حل قريب منه المهم أن يكون حلا صالحا للاستخدام.
- التبسيط(Simplification): غالبًا ما تكون أسهل في الفهم والتطبيق.
- التعلم من التجربة(Learning from Experience): تستفيد من النتائج السابقة لتحسين الأداء في المحاولات اللاحقة.
- المرونة(Flexibility): تعمل في مختلف البيئات والمواقف.
- الاستدلال(Inference): تستخدم قواعد منطقية بسيطة لاتخاذ قرارات سريعة.
اقرأ أيضا: آفاق الإبداع، العقل البشري والذكاء الاصطناعي.
أنواع الخوارزميات الاستكشافية:
- خوارزميات البحث المحلي(Local Search Algorithms): تبدأ هذه الخوارزميات من حل أولي وتحاول تحسينه تدريجياً. مثال على ذلك خوارزمية تسلق التل(Hill Climbing Algorithm)، التي تشبه تسلق جبل في الضباب، حيث نتحرك دائماً نحو الاتجاه الأعلى.
- خوارزميات التطور(Evolutionary Algorithms): تستوحي هذه الخوارزميات من نظرية التطور في الطبيعة. الخوارزميات الجينية(Genetic Algorithms) هي مثال شهير، حيث تتطور الحلول عبر الأجيال من خلال عمليات تشبه التزاوج والطفرات الجينية.
- خوارزميات الذكاء الجماعي(Swarm Intelligence Algorithms): تستلهم هذه الخوارزميات سلوك الحشرات والحيوانات التي تعمل في مجموعات. خوارزمية مستعمرة النمل(Ant Colony Optimization) مثلا تحاكي طريقة النمل في إيجاد أقصر الطرق للغذاء.
- خوارزميات البحث التابو(Tabu Search): تستخدم هذه الخوارزميات “قائمة محرمات” لتجنب العودة إلى حلول سبق استكشافها، مما يساعد في استكشاف مناطق جديدة من فضاء الحل.
- خوارزميات التبريد التدريجي(Simulated Annealing): مستوحاة من عملية تبريد المعادن في الصناعة، تسمح هذه الخوارزميات بقبول حلول أسوأ أحياناً لتجنب الوقوع في الحلول المحلية الأمثل(Local Optima).
تطبيقات الخوارزميات الاستكشافية:
نظرا للطبيعة العملية للخوارزميات الاستكشافية، يمكن استخدامها في العديد من المجالات، أشهرها:
- تخطيط المسارات(Route Planning): تُستخدم في تطبيقات الخرائط والملاحة لإيجاد مسارات فعالة بين نقطتين.
- جدولة الموارد(Resource Scheduling): في إدارة المشاريع وتخطيط الإنتاج، تساعد في عملية توزيع الموارد بكفاءة.
- تصميم الدوائر الإلكترونية(Circuit Design): تُستخدم في تحسين تصميم الرقائق الإلكترونية المعقدة.
- التعرف على الأنماط(Pattern Recognition): في مجالات مثل معالجة الصور والتعرف على الكلام.
- تحسين الشبكات(Network Optimization): في تصميم وإدارة شبكات الاتصالات وشبكات الكمبيوتر.
- الذكاء الاصطناعي وتعلم الآلة(AI and Machine Learning): تُستخدم في تدريب النماذج وتحسين أدائها.
مزايا وتحديات الخوارزميات الاستكشافية:
ككل التقنيات المخترعة من قبل البشر توجد مزايا وعيوب للخوارزميات الاستكشافية، هذه المزايا والتحديات يجب معرفتها بشكل دقيق لاختيار الخوارزمية الأكثر ملائمة للمشكلة التي نتعامل معها للوصول إلى حلول مقبولة وذات جدوى معقولة.
المزايا:
- السرعة: توفر حلولاً سريعة للمشكلات المعقدة.
- المرونة: يمكن تطبيقها على مجموعة واسعة من المشكلات.
- الفعالية: غالباً ما تجد حلولاً جيدة جداً، وإن لم تكن مثالية.
التحديات:
- عدم ضمان الحل الأمثل: قد لا تصل دائماً إلى أفضل حل ممكن.
- الاعتماد على المعلمات: أداؤها قد يتأثر بشدة بإعدادات المعلمات وقيمها الأولية.
- صعوبة التمثيل الرياضي: يصعب أحياناً تحليل أدائها أو نمذجتها بشكل رياضي دقيق.
كيفية اختيار وتطبيق الخوارزمية الاستكشافية:
تمر عملية اختيار الخوارزمية الاستكشافية المناسبة لأي مشكل بالخطوات التالية:
- فهم المشكلة: حدد بدقة ما تحاول حله وما هي القيود المرافقة.
- تقييم الموارد: انظر في الوقت والقدرة الحاسوبية المتاحة.
- دراسة الخيارات: اطلع على مختلف أنواع الخوارزميات الاستكشافية وتطبيقاتها.
- التجربة والمقارنة: جرب عدة خوارزميات وقارن أداءها على مشكلتك المحددة.
- التحسين: قم بضبط معلمات الخوارزمية المختارة لتحسين أدائها.
- التحقق: تأكد من أن الحلول المقدمة تلبي متطلبات مشكلتك.
مثال تطبيقي: مشكلة البائع المتجول (Traveling Salesman Problem):
لنأخذ مثالاً شهيراً: مشكلة البائع المتجول، تخيل بائعاً يحتاج لزيارة عدة مدن مرة واحدة والعودة إلى نقطة البداية، مع محاولة تقليل المسافة الإجمالية. هذه المشكلة معقدة للغاية عندما يزداد عدد المدن، ولا توجد خوارزمية مضمومة لحلها.
يمكن استخدام خوارزمية استكشافية مثل خوارزمية النمل (Ant Colony Optimization) لحل هذه المشكلة وفق التالي:
- تمثيل المدن كنقاط على خريطة.
- إنشاء “نمل” افتراضي يتحرك بين المدن.
- كل “نملة” تترك أثراً (فيرمون) على المسار الذي تسلكه.
- المسارات الأقصر تجمع فيرمون أكثر مع الوقت.
- النمل اللاحق يميل لاتباع المسارات ذات الفيرمون الأعلى.
- مع تكرار العملية، يتم اكتشاف مسارات أكثر كفاءة.
هذه الطريقة لا تضمن إيجاد أقصر مسار مطلق، لكنها غالباً ما تجد مساراً جيداً جداً في وقت معقول.
الخاتمة:
الخوارزميات الاستكشافية هي أدوات قوية في عالم البرمجة وحل المشكلات. إنها تمثل توازناً ذكياً بين الدقة والسرعة، مما يجعلها مناسبة للعديد من التطبيقات في العالم الحقيقي. ومع تطور التكنولوجيا وزيادة تعقيد المشكلات التي نواجهها، من المرجح أن تزداد أهمية هذه الخوارزميات في المستقبل.
بينما تستمر الأبحاث في تطوير خوارزميات استكشافية جديدة وتحسين القائمة منها، يبقى التحدي الأكبر هو اختيار وتطبيق الخوارزمية المناسبة لكل مشكلة محددة. فهم أساسيات هذه الخوارزميات ومبادئها يساعد المبرمجين والمهندسين على اتخاذ قرارات أفضل في تصميم وتنفيذ الحلول البرمجية.
في النهاية، الخوارزميات الاستكشافية ليست مجرد أدوات تقنية، بل هي طريقة للتفكير. إنها تعلمنا أن الحلول الجيدة يمكن أن تأتي من التفكير الإبداعي والتجربة، وليس فقط من الحسابات الدقيقة. وهذه الفكرة قابل للتطبيق ليس فقط في عالم البرمجة، بل في مختلف جوانب حياتنا اليومية.







لا توجد تعليقات